It is my suspicion that the primary reason people do not develop a working knowledge of music theory is not because they don’t initially understand the basic concepts, but because they do not memorize the information that is derived from the concepts. Example: In the previous entry, we learned the names of the notes that are utilized in Western Music (C, C#/Db, D, etc….) and the names of the intervals  between these notes. (minor second, major second, etc.) But it is not enough to have a general understanding of these concepts. We need to have a working knowledge of these concepts if we are to proceed. This requires memorization.

Let’s take another example that we can all relate to. Let’s say we want to understand a higher math, such as Algebra. If we only understand the concepts of addition, subtraction, multiplication, and division, we will not be able to follow the discussions that occur in an Algebra class. None of us go in to an Algebra class understanding only the concepts of basic math. We actually have to have these concepts memorized. Meaning, we have to memorize basic multiplication tables, sums of number pairs, and the like. We need know what 9+2 is without having to think about it. If we were in an advanced math class and we had to stop and think about the answers to basic math questions such as these, we would make no progress whatsoever. We’d be lost, and if we were not able to identify lack of memorization as the problem, we’d begin to think we lacked the capacity to learn the higher math.

Likewise with music theory. If we have to stop and figure out what a major third above D-flat is every time it was mentioned, well, let’s face it, we’re not going to stand a very good chance of following the conversation.  We need to not only know about the general concepts covered in the previous post, we need to really know them. We need to commit them to memory. This is because we’re going to take these basic building blocks and use them to assemble more and more complicated musical structures.

When I was trying to learn these basic concepts, I made flashcards. I simply committed all the basic stuff to memory, and it really didn’t take very long. If we consider learning the intervals between notes (i.e., what note is a Perfect Forth up from C? What note is a minor second up from Db?) it’s really not that much memorization, and it will probably go further in helping us gain a working knowledge of music theory that any other exercise.

However, instead of simply committing this information to memory without any other reference point, I suggest we kill two birds with one stone, and hinge this memorization exercise to another.

In the previous post, I asked you to memorize only the following intervals:

1 whole step = Major Second

2 whole steps = Major Third

2 1/2 whole steps = Perfect Fourth

3 1/2 steps = Perfect Fifth

4 1/2 steps = Major Sixth

5 1/2 steps = Major 7th

6 whole steps = Octave

Here they are on a piano:

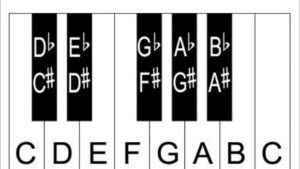
The reason I asked you to memorize these intervals is that these intervals make up what we call the Major Scale

We’ll dive into a full blown discussion of what the major scale is momentarily, but for now, just work through the following exercise with me:

Write down C on a piece of paper.

Write down the note that is a Major Second up from C.

Write down the note that is a Major Third up from C.

Write down the note that is a Perfect Fourth up from C.

Write down the note that is a Perfect Fifth up from C.

Write down the note that is a Major 6th up from C.

Write down the note that is a Major 7th up from C.

Write down the note that is an Octave up from C.

You should have the following notes:

C D E F G A B C

What you’ve written down is the C major scale. Congratulations.

Now, let’s do the same thing starting from G.

Write down G on a piece of paper.

Write down the note that is a Major Second up from G.

Write down the note that is a Major Third up from G.

Write down the note that is a Perfect Fourth up from G.

Write down the note that is a Perfect Fifth up from G.

Write down the note that is a Major 6th up from G.

Write down the note that is a Major 7th up from G.

Write down the note that is an Octave up from G.

You should have:

G A B C D E F# G

Note that the intervals from the first note of the major scale to any of the other notes in the major scale are either Major or Perfect. None of them are minor or diminished or augmented or any of that other weird stuff. So, instead of memorizing ALL of the intervals between ALL of the notes, I suggest we memorize every major scale in every key, and use this as our tool to start memorizing intervals. Why? First, because this is practical knowledge that we really need. It’s not esoteric. We need to know the major scales cold. Second, because this is actually easier, and it involves less memorization.

Here’s how this works. Let’s look at C major for a moment. It’s pretty easy to memorize. Memorize it right now. It’s C D E F G A B C. Now memorize the intervals that are used to build a major scale. If we start from C, and go up a Major Second (1 whole step) we get D. If we start from C and go up a Major Third (2 whole steps) we get E. If we start from C and go up a perfect fourth (2 1/2 steps) we get F. If we start from C and go up a perfect fifth (3 1/2 steps) we get G. If we start from C and go up a Major Sixth (4 1/2 steps) we get A. If we start from C and go up a Major Seventh (5 1/2 steps) we get B. If we start from C and go up an octave (6 steps) we get C.

Look at the piano one more time to verify this:

If we really consider all of this information carefully, we have learned a lot about the C major scale. We not only know the notes in the C major scale, but we know the names of the intervals from the first note (C) to the other notes in the scale. Now let’s reverse that logic, and ask ourselves this: What is a Perfect Fifth up from C? All we have to do is name the fifth note of the C major scale. We don’t have to go through all of the craziness of counting steps (uh…let’s see….a perfect fifth is….uh…where are my notes?…. 3 1/2 steps, so…C…to C#…that’s a half step…and then…uh…wait where was I? What was the question again?)

Let’s try it some more:

What’s a Major Second up from C?

What’s a Major Third up from C?

What’s a perfect fourth up from C?

What’s a perfect fifth up from C?

What’s a Major Sixth up from C?

What’s a Major Seventh up from C?

What’s an Octave up from C?

In each case, you simply name the note that corresponds with the proper number.

What’s a Major Second up from C?

From the first note to the second note of a major scale is a Major Second. The second note of the C major scale is D. The answer is D.

What’s a Major Third up from C?

From the first note to the third note of a major scale is a Major Third. The third note of the C major scale is E. The answer is E.

What’s a perfect fourth up from C?

From the first note to the fourth note of a major scale is a Perfect Fourth. The Fourth note of the C major scale is F. The answer is F.

What’s a perfect fifth up from C?

The answer is G.

What’s a Major Sixth up from C?

The answer is A.

What’s a Major Seventh up from C?

The answer is B.

What’s an Octave up from C?

The answer is C.

Now, of course, you can set this method aside, and just memorize the every interval between every note if you so choose. This is just one way to think about it, and the way that I have happened to think about it for years. But that doesn’t mean it’s the only way.

If we do accept the logic of this method, then we need to complete one task. We need to memorize every major scale, which we’ll do in our next blog entry.  If you’d like to start drilling yourself on intervals now, I have made a simple test for you to practice with. You’ll need Microsoft Excel to open this file. You can download it by  clicking here.